Mathematical Combat Distance

1/27/07

Intuitively, one understands that danger is inversely proportional to the distance from a threat. In the martial arts, this concept of "combative distance" is crucial.

This informal article will outline one way of looking at combat distance. I've personally found it useful, and hope others can.

Let's represent each Person_i by a circle of radius Leg_i and concentric circle of radius Arm_i. The center of the circle is the center of a person; their center of gravity, core, tanden, tantien, etc.

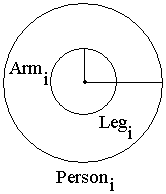
Each radius is the reach of the arm and leg respectively, and the extent of each reach is marked by the edge of the circle. Note that these distances can be measured for any person. Simply stand stationary, extend a limb, and have someone measure the distance the limb extends, using a measuring tape.

What happens when two people, who are a distance, d, apart, approach each other? The outcome (keep in mind our assumptions, listed at the end of the article), hinges on two factors

1. How does Leg₁ compare to Leg₂?
2. How does Arm₁ compare to Arm₂?

Consider

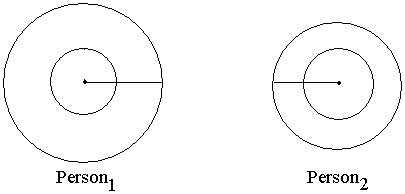
If these people approach (cross your eyes to make them approach), Person₁ is able to touch Person₂'s center first or able to "cover" a larger fraction of Person₂. How can we mathematically express this?

Note that when Person₁ is able to do this, more of Person₂ is overlapped by Person₁ than vice versa. This overlap, expressed mathematically as a measure of area, is

Therefore, the percentage overlap of Person₂ is the overlap divided by Person₂'s area, or

Let's label this number by LegDanger₂, and note that if LegDanger_i > LegDanger_j, then Person_i is in more trouble than Person_j from leg attacks.

Note, however, that if Person₁'s leg attack fails, then Person₂'s arm attack is able to get to Person₁'s center first, barely. This is why one must take into account both leg and arm attacks. The above formula for A is calculated using the Arm radii, and we get ArmDanger₁ and ArmDanger₂ respectively.

Therefore, Person₁'s total danger is

Written out in full, this is

For a given time in an encounter, one can compare Danger₁ and Danger₂. If Danger₁ > Danger₂, then Person₁ is, theoretically, in trouble.

The discussion has been held to open-hand combat. Most weapons could be included in the Arm radius. However, a weapon like a gun would have a huge radius, hundreds of feet, and its circle would easily overlap any non-weapon carrying person.

What happens with multiple opponents? Say Person₁ is being attacked by Person₂ and Person₃

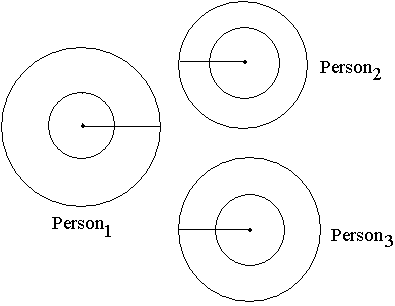
To assess danger, we'd compare Danger₁ to Danger₂ + Danger₃.

In this article, there are several assumptions that are needed so we can talk about such a simple model

• model is 2-dimensional. One could consider doing the same analysis using spheres and volumes
• each person can attack and defend 360 degrees
• beside arm and leg reach, each person is equal in all other aspects
• attacking or controlling the opponent's center is the goal, and is most devastating

I think looking at overlapping circles of various radii is the simplest case of developing a model to help explain combat distance. It has the bonus of everything being measurable, and explains the common sense of why fighting against weapons and multiple attackers is very, very difficult.